Was ist am Fadenpendel eigentlich harmonisch?
Kurzfassung
In der Stunde soll der Bewegungsvorgang beim Fadenpendel untersucht und die notwendigen Randbedingungen, welche die Beschreibung als harmonische Schwingung gestatten, erarbeitet werden. Im Rahmen eines Schülerexperiments messen die Schüler mit ihren eigenen Smartphones die tangentiale Beschleunigung und erleben die Kleinwinkelnäherung anhand der graphischen Auswertung des Experiments, ohne dass diese näher mathematisch thematisiert wird.
Im Anschluss an die Stunde wird das Fadenpendel unter Beachtung der Kleinwinkelnäherung mathematisch beschrieben und die Bewegungsgleichungen aufgestellt. Als Ausblick kann hier nun die allgemeine Beschreibung durch die Methode der kleinen Schritte erfolgen und auch einige Sonderfälle diskutiert werden.
Sachanalyse
Unter einer Schwingung versteht man einen Bewegungsvorgang, bei dem ein System aus seiner stabilen Gleichgewichtslage ausgelenkt wird und dabei eine rücktreibende Kraft erfährt. Die maximale Auslenkung aus der Ruhelage wird als Amplitude und die Dauer für eine vollständige Schwingung als Schwingungsdauer bezeichnet. Sind Amplitude und Schwingungsdauer zeitlich konstant, spricht man von einer (ungedämpften) periodischen Schwingung; Wenn die rücktreibende Kraft zu jedem Zeitpunkt proportional zur momentanen Auslenkung ist, so handelt es sich um eine harmonische Schwingung.
Bei der Beschreibung des Fadenpendels wird im schulischen Alltag angenommen, dass keine Form der Reibung auftritt und dass die gesamte Masse des Pendels in einem einzigen Punkt im Abstand l von Drehpunkt konzentriert ist. Diese Idealisierung wird als mathematisches Pendel bezeichnet, während beim physikalischen Pendel die reale Massenverteilung berücksichtigt wird.
Auch wenn die Bewegung des schwingenden Massestücks auf einer zweidimensionalen Bahn erfolgt, besitzt der Bewegungsvorgang nur einen Freiheitsgrad und ist durch die Größe des Auslenkungswinkels φ oder durch Bogenlänge s eindeutig beschrieben. Durch die Kräftezerlegung des ausgelenkten Pendels erhält man die Kraftgleichung
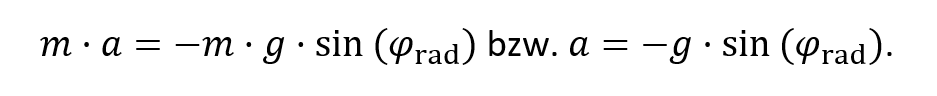
Da für die harmonische Schwingung die Proportionalität der rücktreibenden Kraft zur Auslenkung gegeben sein muss, kann das das Fadenpendel nur in dem Bereich als harmonische Schwingung modelliert werden, in dem die Kleinwinkelnäherung sin(φ) = φ hinreichend gut erfüllt ist. Nur unter dieser Näherung ist eine exakte Lösung der Kraftgleichung möglich, in allen anderen Fällen ist die Gleichung nur numerisch lösbar.
Als exakte Lösung erhält man bei einer Startgeschwindigkeit von 0 für die Winkelabhängigkeit die Funktion φ(t) = φ(0)·cos(ωt).
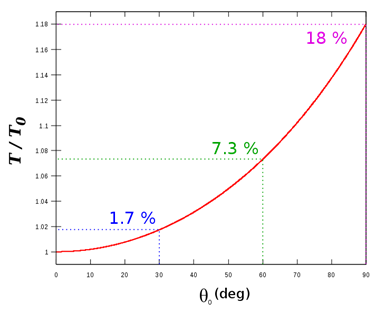
Für größere Startauslenkungen kann die Schwingungsdauer durch folgende Reihenentwicklung bestimmt werden. Die prozentuale Abweichung zwischen der korrekten Periodendauer und dem Wert, der bei fälschlicher Annahme der Kleinwinkelnäherung berechnet würde, wird in durch die untenstehende Abbildung veranschaulicht:
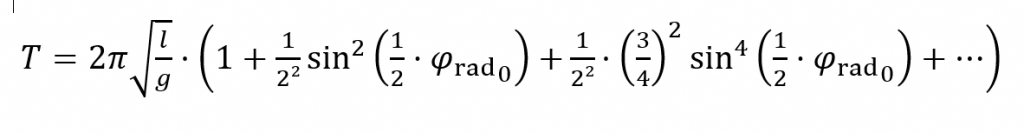
Didaktische Analyse
Ein zu mathematischer Zugang über die Kleinwinkelnäherung erscheint aus einem anderen Ansatzpunkt her didaktisch bedenklich und für Fehlvorstellungen anfällig zu sein: Wenn beim Fadenpendel nicht sehr exakt zwischen dem Sinus zur Beschreibung der rücktreibenden Kraft in Abhängigkeit des Auslenkwinkels und der Sinusfunktion zur Beschreibung der Auslenkung in Abhängigkeit der Zeit unterschieden wird, kann für den Schüler folgender (falscher) Zirkelschluss entstehen: Wir stellen den Kraftansatz a = – g·sin(φ) auf und vereinfachen ihn unter Verwendung der Kleinwinkelnäherung sin(φ) = φ zum Ansatz a = -g·φ. Da es sich jetzt um eine harmonische Schwingung handelt, ist die Lösung der Bewegungsgleichung eine Sinusfunktion. Aber wir haben doch gerade den Sinus genähert und weggelassen???
In der vorgeschlagenen Stunde soll den Schülern die Möglichkeit gegeben werden, die rücktreibende Kraft als Ursache der Pendelbewegung sowie deren Proportionalität innerhalb eines gewissen Bereichs als Kriterium für die Beschreibung als harmonische Schwingung zu begreifen. Dieser Ansatz basiert auf der eigentlichen Definition der harmonischen Schwingung, welche aufgrund von messtechnischen Schwierigkeiten für das Fadenpendel oft vernachlässigt und nur die Periodendauer im Experiment untersucht wird.
Die Messung der rücktreibenden Kraft erfolgt dabei über die entsprechende Beschleunigung, welche mit einem Smartphone gemessen wird. Moderne Geräte besitzen Beschleunigungssensoren, deren Messdaten über verschiedene Programme als 3D Beschleunigungsvektoren ausgelesen werden können. Mittlerweile existiert eine Vielzahl an Programmen, lassen Sie Ihr Schüler hier selber recherchieren.
Die folgenden Abbildungen zeigen den schematischen Experimentaufbau und die graphische Auswertung der Messung. Die lineare Annäherung bestätigt die bekannte Faustregel für die Kleinwinkelnäherung.
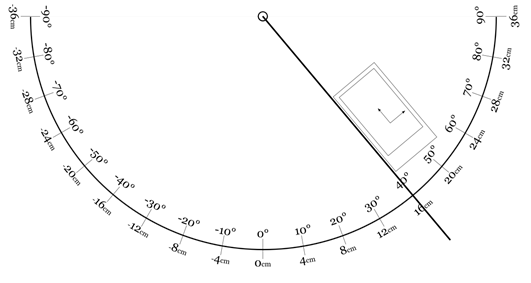
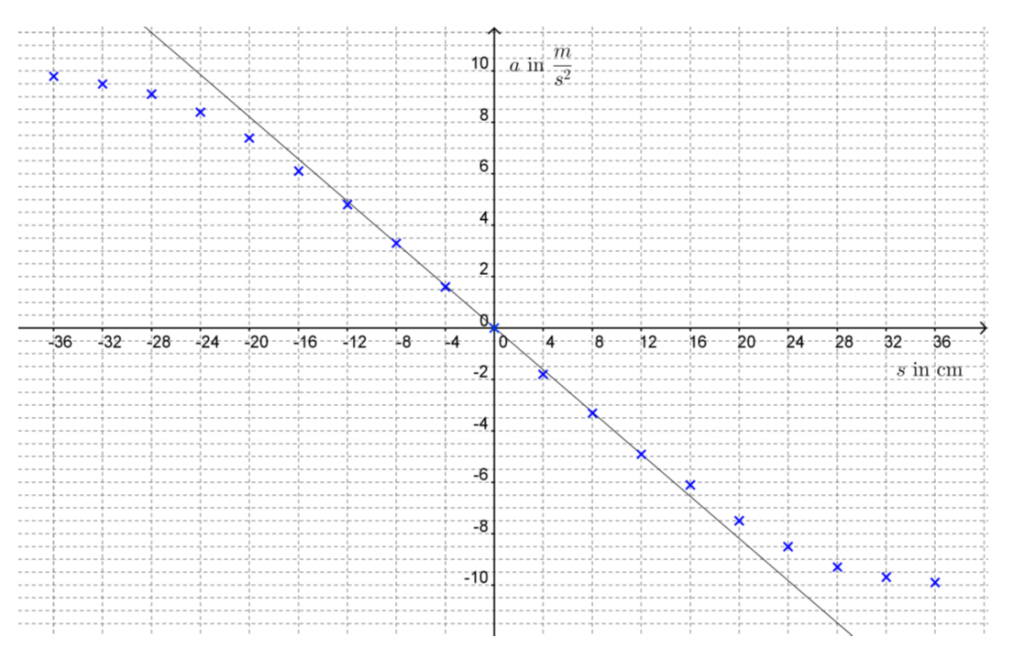
Verwendetes Material und Ablauf
Die Schüler arbeiten z.B. in Dreiergruppen. Dies muss auf die Anzahl der vorhandenen Geräte in der Klasse abstimmt werden. Anhand des Aufbaus messen die Schüler die für die rücktreibende Kraft entscheidende tangentiale Beschleunigung in Abhängigkeit von der Auslenkung und werten dies graphisch aus (vgl. Arbeitsblatt bzw. Lösung dazu). Das zugehörige Arbeitsblatt enthält alle für die Durchführung und die erste Auswertung nötigen Handlungsabfolgen. Jede Gruppe trägt die Daten in ein Arbeitsblatt ein. Dieses wird am Ende der Stunde eingesammelt und für die restlichen Schüler der Gruppe kopiert.
Die Kopiervorlage für den Aufbau liegt in zwei Versionen vor: Dabei wurde der Radius des Aufbaus jeweils so gewählt, dass 10° in „Winkelskala3m.pdf“ einer Bogenlänge von 3cm und in „Winkelskala4cm.pdf“ einer Bogenlänge von 4cm entsprechen, so dass sich für die Auslenkung im Winkelmaß sowie für die Bogenlänge im Rahmen der Messgenauigkeit immer ganze Zahlenwerte ergeben. Winkelskala3cm kann auf DinA3-Papier kopiert, laminiert und dann entweder auf einem Holzaufbau befestigt oder auch „an die Wand geklebt“ werden. Winkelskala4cm ist für DinA3 zu groß, aber schöner zu handhaben. Es bietet sich an, sechs Skalen auf einem DinA0-Plotter zu drucken, dafür ist die Vorlage „Skalen auf A0-Poster.pdf“ bereitgestellt.
Anstelle eines Pendels wird nur ein einfacher Faden montiert, der von den Schülern an die gewünschte Auslenkposition gezogen werden kann und als Orientierung für die Neigung des Smartphones dient. Das verwendete Stativmaterial sollte ausreichend stabil sein, dass durch das Andrücken des Geräts keine Verkippung des Aufbaus und damit keine größeren Messfehler entstehen sollten.
Für die Messung der Beschleunigung verwenden die Lernenden eine geeignete App, welche mittlerweile in (unerübersehbarer) Hülle und Fülle verfügbar sind. Lassen Sie die Lernenden hier sich ergebnisoffen für eine App entscheiden und diskutieren Sie im Anschluss über Vor- und Nachteile der verschiedenen Programme (zeitliche Auflösung, graphische Darstellung, Einstellmöglichkeiten etc.).
Für meinen Prototypen habe ich 12 Aufbauten mit Material aus dem Baumarkt gebaut, die Kosten lagen inklusive Druck bei ca. 120 Euro. Kosten für die Messgeräte bestehen keine.
Bedeutung der Inhalte für die Schüler
Die mannigfaltigen Möglichkeiten des eigenen Smartphones stellen für viele Schüler eine große Versuchung dar, sich im Unterricht fremd zu beschäftigen. Wenn Schüler jedoch anstatt eines „Handy weg“ ein „Handy raus“ hören, schafft dies eine ungewohnte Abwechslung und wirkt sich ungemein motivationsfördernd aus und sensibilisiert die Schüler zudem für die Allgegenwärtigkeit der Physik im Alltag und den technischen Geräten. Darüber hinaus eröffnet dies dem häufig knapp budgetierten Physikunterricht neue Möglichkeiten, da die Messgeräte von den Lernenden selbst finanziert und mitgebracht werden.
Dass sich die beschriebene Software in dieser Klasse einsetzen lässt und sich positiv auf das Lernklima auswirkt, konnte ich auch an anderer Stelle erfahren. In einer der vorangegangenen Stunden nutzten die Schüler ihr Smartphone, um die Kräftezerlegung an einer schiefen Ebene zu messen und mit einer Vergleichskonstruktion und –messung zu bestätigen. Vor allem die Zerlegung der wirkenden Kraft in drei Komponenten sowie das Drehen des Koordinatensystems durch Drehen des Handys war beim ersten Mal für viele Schüler herausfordernd.
Die Vorgänge beim Fadenpendel können leicht auf Vorgänge aus dem Schüleralltag übertragen werden, wie z.B. das Schaukeln oder das Analogmetronom. Zudem wird das Wissen um die harmonische Schwingung vertieft, welches im Verlauf des Schuljahres noch im Bereich der Akustik von Bedeutung sein wird.
Das Fadenpendel als Beispiel für eine (teilweise) harmonische Schwingung zeigt zudem den Schülern in eindrucksvoller und erlebbarer Weise die Natur und das Selbstverständnis der Physik auf: Die Modellierung der Natur durch die Mathematisierung gilt nur innerhalb gewisser Grenzen des Models und muss bei der Überschreitung dieser durch eine neue – bessere – Beschreibung ersetzt werden. Dieser Aspekt, der zu einem späteren Zeitpunkt des Lehrplans den Übergang zur Relativitätstheorie schlägt, kann hier bereits betont werden.
Die hinterlegten Materialien können für schulische Zwecke kostenfrei verwendet werden. Bei anderweitiger Verwendung bitte ich um Rücksprache unter didactics (a) diplomer.de.
Ich wünsche Ihnen viel Spaß bei der Durchführung
Dr. Michael Plomer
Beitrag verfasst von: Michael Plomer
